“MỌI SỰ CỐ GẮNG CHƯA CHẮC ĐÃ GẶT GÁI ĐƯỢC KẾT QUẢ NHƯNG MỖI KẾT QUẢ ĐẠT ĐƯỢC CHẮC CHẮN LÀ CẢ MỘT QUÁ TRÌNH CỐ GẮNG”

Bài tập chủ đề số học, lệnh điều kiện, lệnh lặp

Thứ tư - 03/01/2024 19:46
Bài tập chủ đề số học, câu lệnh điều kiên, câu lệnh lặp
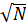
Bài tập chủ đề số học, lệnh điều kiện, lệnh lặp
Câu 1. (5,0 điểm):
Cho biểu thức:
T=1+2 – 3+ 4+ 5-6 +7 +8-9+ 10+ 11-12 +13 + ...
Dễ thấy biểu thức T là tổng các số tự nhiên không chia hết cho 3 rồi trừ các số tự nhiên chia hết cho 3.
Cho số N, em hãy tính giá trị của biểu thức T theo quy luật trên, là tổng và hiệu của các số tự nhiên không quá N.
Dữ liệu vào: Đọc vào từ tệp Caul.inp
Ghi duy nhất một số N (1 ≤ N ≤ 109).
Kết quả ra: Ghi ra tệp Caul.out
Ghi ra giá trị của biểu thức T.
Ví dụ:
Caul.inp Caul.out Giải thích
3 0 T=1+2-3=0
7 10 T=1+2 – 3+ 4+ 5-6 + 7 = 10
Có 80 % test có N  ≤ 104;
Có 20% test có 108 ≤ N ≤ 109.
Câu 2. (5,0 điểm)
Hôm nay, học về tính chia hết của số tự nhiên, Bờm biết rằng nếu A chia hết cho B thì A chia B dư 0, hay ta còn nói rằng B là ước của A.
Thầy giáo giao cho Bờm một bài tập như sau:
Cho hai số tự nhiên N,M (1<N<M< 1014), hãy đếm xem từ N đến M có bao nhiêu số mà có số ước là số lẻ và bản thân số M thì có bao nhiêu ước?
Dữ liệu vào: Đọc vào từ tệp Cau2.inp
Ghi hai số tự nhiên N, M.
Kết quả ra: Ghi ra tệp Cau2.out
Dòng đầu ghi số lượng các số tự nhiên thuộc [N, M] mà có lẻ ước. Dòng thứ hai ghi số ước của số M.
Ví dụ:
Cau2.inp Cau2.out Giải thích
1 4 2
3		 Có hai số có lẻ ước từ 1 đến 4 là số 1 và số 4; Số 4 là số có 3 ước.
Có 80% số test có 1 ≤ N ≤   M ≤ 104;
Có 20% số test có 109  ≤ N ≤ M ≤ 1014
Câu 3: (5.0 điểm)
Số 4 được coi là anh em với số B nếu tổng các ước của 4 bằng 8 hoặc tổng các ước của B bằng 4. Chú ý ở đây ta quy định rằng cặp (A, B) và cặp (B, A) chỉ tính là một cặp, A khác B.
Nhập vào số tự nhiên N (N ≤ 3.105). Đếm số cặp anh em trong đoạn [1,N)]
Dữ liệu vào: Đọc từ tệp CAU03.INP gồm một dòng duy nhất chứa số tự nhiên N.
Dữ liệu ra: Ghi ra tệp CAU03.OUT gồm một dòng duy nhất chứa số cặp số anh em trong đoạn [1,N].
          Ví dụ:
CAU03.INP CAU03.OUT Giải thích
10 5 Trong đoạn [1,10] có 5 cặp số anh em là (2, 3) (3, 4); (4, 7); (5, 6); (7, 8)
Có 80% test có N ≤104; Có 20% test có 105 ≤ N ≤ 3.105
Câu 4: (5,0 điểm).
        Nhập vào 2 số tự nhiên A, B. Hãy đếm xem trong đoạn [A, B] có bao nhiêu số nguyên tố?
Dữ liệu vào: Đọc từ tệp CAU04.INP gồm một dòng duy nhất chứa 2 số tự nhiên A, B cách nhau bởi một khoảng trắng, A ≤  B ≤ 107;
Dữ liệu ra: Ghi ra tệp CAU04.OUT gồm một dòng duy nhất chứa số lượng số nguyên tố trong đoạn [A, B]
Ví dụ:
CAU04.INP CAU04.OUT Giải thích
1 10 4 Có bốn số nguyên tố trong đoạn [1,10] là:
2, 3, 5, 7
Có 80% test có 1 ≤ A ≤ B ≤ 105; Có 20% test có 106 ≤  A ≤ B ≤ 107.
Câu 5. (5,0 điểm) SUM
Cho dãy số T = 1.2.3+2.3.4+ ... + n(n + 1)(n + 2) với 1≤ n ≤103)
Yêu cầu: Tính tổng T và tìm chữ số lớn nhất trong tổng T
Dữ liệu vào: Đọc vào từ tệp văn bản SUM.inp
Chỉ có một số nguyên duy nhất (1 ≤ n ≤103)
Kết quả: Ghi ra tệp văn bản SUM.out
- Dòng 1 in ra tổng T
          - Dòng 2 in chữ số lớn nhất trong tổng T
Ví dụ:
SUM.inp SUM.out Giải thích
8 1980
9		 Tổng T=1980,
Chữ số lớn nhất là 9
Subtask 1: 50% test có 1 ≤ n ≤ 300;
Subtask 2: 50% test có 300 < n ≤ 1000.
Câu 6. (5,0 điểm) NUMBER
Một số nguyên dương được gọi là “đẹp” nếu số đó chia hết cho số các ước của số nguyên dương của nó. Ví dụ: số 36 có 9 ước nguyên dương là: 1, 2, 3, 4, 6, 9, 12, 18, 36; mà 36 lại chia hết cho 9, vậy số 36 là số “đẹp”.
Yêu cầu: Cho số tự nhiên n, đếm số lượng các số đẹp nhỏ hơn hoặc bằng n.
Dữ liệu vào: Từ tệp văn bản NUMBER.inp
Ghi một số duy nhất n (1 ≤ n ≤ 105)
Kết quả: Ghi ra tệp văn bản NUMBER out
Số lượng số đẹp nhỏ hơn hoặc bằng n.
Ví dụ:
NUMBER.inp NUMBER.Out Giải thích
40 9 Có các số “đẹp” là: 1, 2, 8, 9, 12, 18, 24, 36, 40
Subtask 1: 50% test có 1 ≤ n ≤ 104;
Subtask 2: 50% test có 104 < n ≤ 105.
Câu 7 (5.0 điểm): Cho biểu thức:
S=1-2 +3-4+5-6 +7-8+9-10+11-12 +13-14 + ...+(-1)n-1.n
Cho số n, em hãy tính giá trị của biểu thức S theo quy luật trên, là tổng và hiệu của các số tự nhiên không quá n.
Dữ liệu vào: Đọc vào từ tệp Cau7.inp
Ghi duy nhất một số n (1 ≤ n ≤ 109).
Kết quả ra: Ghi ra tệp Cau7.out
Ghi ra giá trị của biểu thức S.
Ví dụ:
Cau7.inp Cau7.out Giải thích
3 2 S=1-2+3= 2
7 4 S=1-2+3-4+5-6+7= 4
Có 80 % test có N  ≤ 104;
Có 20% test có 108 ≤ N ≤ 109.
Câu 8. Bắt tay (4,0 điểm)
Trong hội nghị tuyên dương các bạn học sinh giỏi cấp tỉnh năm 2020, có n học sinh tham dự mọi người gặp nhau chào hỏi và bắt tay nhau. Biết rằng mỗi học sinh bắt tay với tất cả những học sinh còn lại và 2 người bất kỳ chỉ được bắt tay nhau đúng 1 lần.
Yêu cầu: Em hãy đếm số lượng cái bắt tay?
Dữ liệu vào: Đọc dữ liệu vào từ tệp BAI08.INP là một số nguyên dương n (1≤ n ≤ 106)
Dữ liệu ra: Ghi kết quả ra tệp BAI08.OUT là số lượng cái bắt tay.
Ví dụ:
BAI08.INP BAI08.OUT
1 0
2 1
3 3
4 6
5 10
Giải thích: Có 1 người thì có 0 cái bắt tay, có 2 người có 1 cái bắt tay, 3 người có 3 cái bắt tay.
Câu 9. Số đảo nguyên tố (4,0 điểm):
Cho số nguyên dương N, khi đảo ngược trật tự các chữ số của N ta sẽ thu được một số nguyên dương M, M được gọi là số đảo ngược của N.
Ví dụ: N= 613 thì M = 316 là số đảo ngược của N.
Số nguyên dương M được gọi là số nguyên tố nếu nó chỉ có hai ước số là 1 và chính nó, số 1 không phải là số nguyên tố.
Cho hai số nguyên dương P và Q với 0 <P<0>105.
Yêu cầu: Hãy tìm tất cả các số nguyên dương N thỏa mãn P<N<Q mà số đảo ngược của số N là số nguyên tố.
Dữ liệu vào: Đọc dữ liệu vào từ tập BAI09.INP
Một dòng ghi hai số nguyên dương P Q, hai số được ghi cách nhau ít nhất một dấu cách.
Kết quả ra: Ghi kết quả ra tệp BAI09.OUT
Gồm nhiều dòng, mỗi dòng ghi một số nguyên N tìm được.
Ví dụ:
BAI09.INP BAI09.OUT
10 19 11
13
14
16
17
Câu 10. (6 điểm) Đếm số ước dương
Cho số nguyên dương N. Hãy đếm số lượng các ước dương của N.
Dữ liệu cho trong tệp văn bản DemUoc.Inp gồm một số nguyên dương N.
Kết quả ghi ra tệp văn bản DemUoc.Out là số lượng các ước dương của N.
Vi du:
DemUoc.Inp DemUoc.Out Giải thích
6 4 6 có các ước dương: 1, 2, 3, 6. => Số lượng các ước dương là 4
Giới hạn:
Có 75% số test ứng với 75% số điểm thỏa mãn 1 < N <106;
Có 25% số test ứng với 25% số điểm thỏa mãn 106 <N<1012
Câu 11: Bóng đá (6 điểm)
Giải bóng đá hạng cao nhất của các quốc gia hầu hết là thi đấu theo thể thức gặp nhau vòng tròn hai lượt (lượt đi và lượt về). Tuy nhiên, tại mỗi quốc gia số đội tham gia giải là khác nhau, nên số trận cũng khác nhau. Ví dụ: Giải V-League của Việt Nam có 12 đội tham gia, nên tổng số trận thi đấu (cả lượt đi và lượt về) là 132 trận.
Yêu cầu: Tính tổng số trận thi đấu của giải bóng đá mỗi quốc gia khi thi đấu theo thể thức vòng tròn hai lượt (lượt đi và lượt về).
Dữ liệu: Vào từ tệp văn bản CAU11.INP: Một số nguyên dương n duy nhất (3 ≤ n ≤ 50) là số đội bóng tham gia giải.
Kết quả: Ghi ra tệp văn bản CAU11.OUT: Tổng số trận thi đấu của giải.
Ví dụ:
CAU11.INP CAU11.OUT Ghi chú
6 30 Có 6 đội bóng đá tham gia giải. Tổng số có 30 trận thi đấu
12 132 Có 12 đội bóng đá tham gia giải. Tổng số có 132 trận thi đấu
Câu 12: Tổng lấy dư (5 điểm)
Cho ba số nguyên dương a, b, m. Các số cách nhau một ký tự trắng.
Yêu cầu: Tính tổng các số nguyên trong đoạn [a..b], rồi chia kết quả cho m lấy phần dư.
Dữ liệu: Vào từ tệp văn bản CAU12.INP gồm ba số nguyên dương a, b, m (1 ≤ a < b≤105; 1 < m ≤ 109).
Kết quả: Ghi ra tệp văn bản CAU12.OUT số dư tìm được.
Ví dụ:
CAU12.INP CAU12.OUT Ghi chú
3 6 7 4 Ta có 3+4+5+6 = 18 chia 7 dư 4
13 19 21 7 Ta có 13+14+15+16+17+18+19 = 112 chia 21 dư 7
Câu ...

 

Tác giả: Vàng Văn Quyn

Tổng số điểm của bài viết là: 0 trong 0 đánh giá

Click để đánh giá bài viết

Những tin mới hơn

Những tin cũ hơn

Tin xem nhiều
Thông tin mới
licham.net

- Click vào nút hiển thị ngày trong tuần hoặc tháng âm lịch để xem chi tiết

- Màu đỏ: Ngày tốt

- Xanh lá: Đầu tháng âm lịch

- Màu vàng: Ngày hiện tại

Thống kê
  • Đang truy cập82
  • Hôm nay2,393
  • Tháng hiện tại67,033
  • Tổng lượt truy cập1,892,778
Chúng tôi đang sử dụng cookie để cung cấp cho bạn những trải nghiệm tốt nhất trên trang web này. Bằng cách tiếp tục truy cập, bạn đồng ý với Chính sách thu thập và sử dụng cookie của chúng tôi.
Bạn đã không sử dụng Site, Bấm vào đây để duy trì trạng thái đăng nhập. Thời gian chờ: 60 giây